American Invitational Mathematics Examination AIME代考

Time Remaining: 2:59:53

Problems Answered: $0 / 15$

Status: Answers Saved

1. AIME I

All answers are integers ranging from 0 to 999 , inclusive.

You should enter a single number consisting of up to 3 digits in each

blank.

Leading zeros are optional.

$1 .$

Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients of 2 and $-2$, respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53)$. Find $P(0)+Q(0)$. $2 .$

Find the three-digit positive integer $a b c$ whose representation in base nine is $b c a$ nine, where $a, b$, and $c$ are (not necessarily distinct) digits.

$3 .$ In isosceles trapezoid $A B C D$, parallel bases $\overline{A B}$ and $\overline{C D}$ have lengths 500 and 650 , respectively, and $A D=B C=333$. The angle bisectors of $\angle A$ and $\angle D$ meet at $P$, and the angle bisectors of $\angle B$ and $\angle C$ meet at $Q$. Find $P Q$. $4 .$

Let $w=\frac{\sqrt{3}+i}{2}$ and $z=\frac{-1+i \sqrt{3}}{2}$, where $i=\sqrt{-1}$. Find the number of ordered pairs $(r, s)$ of positive integers not exceeding 100 that satisfy the equation $i \cdot w^{r}=z^{s}$.

$5 .$

A straight river that is 264 meters wide flows from west to east at a rate of 14 meters per minute. Melanie and Sherry sit on tha enith hanl of tha riwar inith Malania a dictanna if $\boldsymbol{D} \mathrm{~ m a t a r e ~ d a i n i n c t r a m ~ f r}$ AIME I

swims at 80 meters per minute, and Sherry swims at 60 meters per minute. At the same time, Melanie and Sherry begin swimming in straight lines to a point on the north bank of the river that is equidistant from their starting positions. The two women arrive at this point simultaneously. Find $D$.

$6 .$

Find the number of ordered pairs of integers $(a, b)$ such that the sequence

$$
3,4,5, a, b, 30,40,50
$$

is strictly increasing and no set of four (not necessarily consecutive) terms forms an arithmetic progression. $7 .$

Let $a, b, c, d, e, f, g, h, i$ be distinct integers from 1 to $9 .$ The minimum possible positive value of

$$
\frac{a \cdot b \cdot c-d \cdot e \cdot f}{g \cdot h \cdot i}
$$

can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n .$

$8 .$

Equilateral triangle $\triangle A B C$ is inscribed in circle $\omega$ with radius $18 .$ Circle $\omega_{A}$ is tangent to sides $\overline{A B}$ and $\overline{A C}$ and is internally tangent to $\omega$. Circles $\omega_{B}$ and $\omega_{C}$ are defined analogously. Circles $\omega_{A} \omega_{B}$, and $\omega_{C}$ meet in six points $-$ two points for each pair of circles. The three intersection points closest to the vertices of $\triangle A B C$ are the vertices of a large equilateral triangle in the interior of $\triangle A B C$, and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of $\triangle A B C .$ The side length of the smaller equilateral triangle can be written as $\sqrt{a}-\sqrt{b}$, where $a$ and $b$ are positive integers. Find $a+b$. $9 .$

Ellina has twelve blocks, two each of red $(\mathbf{R})$, blue $(\mathbf{B})$, yellow $(\mathbf{Y})$, green $(\mathbf{G})$, orange $(\mathbf{O})$, and purple $(\mathbf{P})$. Call an arrangement of blocks even if there is an even number of blocks between each pair of blocks of the same color. For example, the arrangement

2. R B B Y G G Y R O P P O

is even. Ellina arranges her blocks in a row in random order. The probability that her arrangement is even is $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

$10 .$ Three spheres with radii 11,13 , and 19 are mutually externally tangent. A plane intersects the spheres in three congruent circles centered at $A, B$, and $C$, respectively, and the centers of the spheres all lie on the same side of this plane. Suppose that $A B^{2}=560$. Find $A C^{2}$.

$11 .$

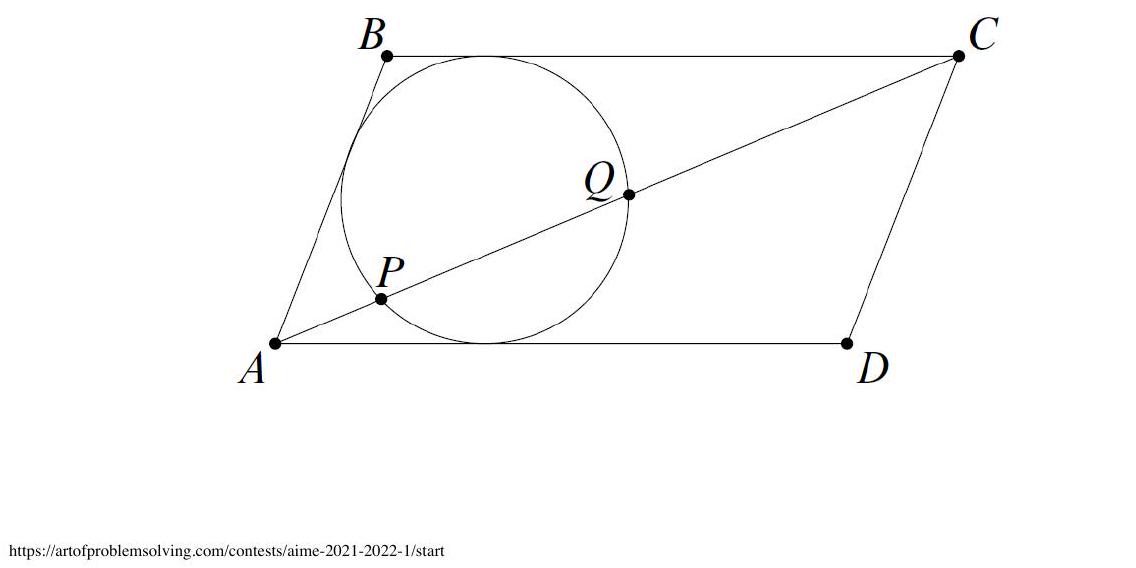
Let $A B C D$ be a parallelogram with $\angle B A D<90^{\circ}$. A circle tangent to sides $\overline{D A}, \overline{A B}$, and $\overline{B C}$ intersects diagonal $\overline{A C}$ at points $P$ and $Q$ with $A P<A Q$, as shown. Suppose that $A P=3, P Q=9$, and $Q C=16$. Then the area of $A B C D$ can be expressed in the form $m \sqrt{n}$, where $m$ and $n$ are positive integers, and $n$ is not divisible by the square of any prime. Find $m+n$.
12

For any finite set $X$, let $|X|$ denote the number of elements in $X$. Define

$$
S_{n}=\sum|A \cap B|,
$$

where the sum is taken over all ordered pairs $(A, B)$ such that $A$ and $B$ are subsets of $\{1,2,3, \ldots, n\}$ with $|A|=|B|$. For example, $S_{2}=4$ because the sum is taken over the pairs of subsets

$$
(A, B) \in\{(\emptyset, \emptyset),(\{1\},\{1\}),(\{1\},\{2\}),(\{2\},\{1\}),(\{2\},\{2\}),(\{1,2\},\{1,2\})\},
$$

giving $S_{2}=0+1+0+0+1+2=4$. Let $\frac{S_{2022}}{S_{2021}}=\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find the remainder when $p+q$ is divided by 1000 . $13 .$

Let $S$ be the set of all rational numbers that can be expressed as a repeating decimal in the form $0 . \overline{a b c d}$, where at least one of the digits $a, b, c$, or $d$ is nonzero. Let $N$ be the number of distinct numerators obtained when numbers in $S$ are written as fractions in lowest terms. For example, both 4 and 410 are counted among the distinct numerators for numbers in $S$ because $0 . \overline{3636}=\frac{4}{11}$ and $0 . \overline{1230}=\frac{410}{3333}$. Find the remainder when $N$ is divided by 1000 .

$14 .$

Given $\triangle A B C$ and a point $P$ on one of its sides, call line $\ell$ the splitting line of $\triangle A B C$ through $P$ if $\ell$ passes through $P$ and divides $\triangle A B C$ into two polygons of equal perimeter. Let $\triangle A B C$ be a triangle where $B C=219$ and $A B$ and $A C$ are positive integers. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and suppose that the splitting lines of $\triangle A B C$ through $M$ and $N$ intersect at $30^{\circ}$. Find the perimeter of $\triangle A B C$. $15 .$

Let $\mathscr{X}, y$, and $z$ be positive real numbers satisfying the system of equations

$$
\begin{aligned}
&\sqrt{2 x-x y}+\sqrt{2 y-x y}=1 \\
&\sqrt{2 y-y z}+\sqrt{2 z-y z}=\sqrt{2} \\
&\sqrt{2 z-z x}+\sqrt{2 x-z x}=\sqrt{3}
\end{aligned}
$$

Then $[(1-x)(1-y)(1-z)]^{2}$ can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n .$

American Invitational Mathematics Examination – AIME

Skip Navigation

• AMC Home
• AIME

AIME

American Invitational Mathematics Examination

Navigation

The AIME (American Invitational Mathematics Examination) is an intermediate examination between the AMC 10 or AMC 12 and the USAMO. All students who took the AMC 12 and achieved a score of 100 or more out of a possible 150 or were in the top 5% are invited to take the AIME. All students who took the AMC 10 and had a score of 120 or more out of a possible 150, or were in the top 2.5% also qualify for the AIME. For the school year the date for the AIME I is , , and the AIME II is , , . There is no additional registration fee for the American Invitational Mathematics Examination, unless you choose to take the second sitting of the exam. An additional administrative/shipping fee is charged, with a minimum of for the first 10 students and for over 10 students. This is explained more thoroughly in the AMC 10/12 and AIME Teacher’s Manuals.

AIME Qualification Changes

Starting in 2011, the qualification parameters will be slightly relaxed for the American Invitational Mathematics Examination (AIME). For students taking the 2012 AMC 10 contests, we will invite students in the top 2.5% of all scorers or scorers with at least 120 points (whichever is more inclusive) to the AIME. This differs from the values of 1% (or 120 points) which have been in effect since 2004. For students taking the 2012 AMC 12, we will invite students in the top 5% of all scorers or scorers with at least 100 points to the AIME. These AMC 12 qualification values remain at the same level they have been since 2000. This policy guards against the possibility of a particularly difficult examination, one on which the scores are uniformly lower than normal, reducing the number of AIME qualifiers.

The requirement is set higher for AMC 10 qualifiers for two reasons:

• First, the AIME can be quite intimidating, and we do not want young students to be discouraged by poor performance on this examination.

• Second, we would like to ensure that any student qualifying for the AIME by virtue of placement on the AMC 10 would likely also qualify for the AIME in subsequent years when taking the AMC 12. It could be very disappointing for a student to be an AIME qualifier in grade 10 but not in subsequent high school years.
By restricting the number of AIME qualifiers from the AMC 10 to the top 2.5%, our plan is to not exclude any very good young students for whom the AIME would be an appropriate experience, but also not put students in a situation where they do not have opportunity to succeed.

Take note: New procedures for the AIME II (Alternate AIME):

The AMC will be using some new procedures for the AIME II (also called the AIME Alternate) this year. Recall that the second (or alternate) date, for the AIME II is , , .

1. The AMC office will mail the 2012 AMC 10 and 2012 AMC 12 reports back to schools starting in late February and continuing until early- to mid-March.  In that AMC 10 and AMC 12 report will be a list of a school’s AIME qualifiers.
2. Included in that report will be AIME I contests (in a sealed envelope) for the school’s  AIME qualifiers, AIME answer forms and the AIME/USAMO Teacher’s Manual. This is the same as we have done for many years.
3. If your AIME qualifiers will be taking the AIME I on , , then everything will be set, you need only follow the directions for the AIME I in the Teachers Manual, and send back the AIME  answer forms for scoring.
4. If your AIME qualifiers will be taking the AIME II on , , then you will still need to fill out the AIME II (or AIME Alternate) registration  either on our webpage (electronic registration) or with the paper form in the AIME Teachers’ Manual. Be sure to include a valid email address.
5. SAVE the AIME Answer forms you receive in the AMC 10/AMC12 report. We will use the same answer forms for both AIME I and AIME II. Also save the AIME Report Envelope, we will use the same AIME Report Envelope for sending back both the AIME I and the AIME II.
6. Watch your email on March 28 for the electronic message containing the AIME II. It will be come as a PDF document attached to the email. Print the AIME II, then make enough copies for each participating AIME II qualifier.
7. Have students taking the AIME II  write “AIME II” in pencil on the top front of the answer form, same side as the answers.
8. Any other necessary directions will be in the AIME Teachers’ Manual.

These new procedures are designed to reduce costs, be faster and more efficient, and more environmentally friendly with less paper and transportation.

Recognition

The AIME is intended to provide further challenge and recognition, beyond that provided by the AMC 10 or AMC 12, to the many high school students in North America who have exceptional mathematical ability. The top scoring U. S. citizens and students legally residing in the United States and Canada (with qualifyng scores, based on a weighted average) are invited to take the USAMO.

Content

The AIME is a 15 question, 3 hour examination in which each answer is an integer number from 0 to 999. The questions on the AIME are much more difficult and students are very unlikely to obtain the correct answer by guessing. As with the AMC 10 and AMC 12 (and the USAMO), all problems on the AIME can be solved by pre-calculus methods. The use of calculators is not allowed.

The AIME provides the exceptional students who are invited to take it with yet another opportunity to challenge their mathematical abilities. Like all examinations, it is but a means towards furthering mathematical development and interest. The real value of the examination is in the learning that can come from the preparation beforehand and from further thought and discussion of the solutions.

Frequently Asked Questions regarding the AIME